Part 1 if you missed it

In part 2 we will be implementing the code for procedures. By the end of this, you will be able to interpret user-defined functions, lambda functions, and something special called “Mu-procedures” that you will soon learn to dislike. This part will be handling problems 6-11. Good luck.

Problem 6: “Begin”

In Scheme, we have the ‘begin’ special form. This lets us evaluate through a series of expressions in scheme and return only the value of the last expression.

It is useful because it allows for side effects from the first expressions to take place while returning only the evaluated value of the last expression in the series. For examples, see the examples in the CS 111 instructions and for even more understanding, read the short documentation for MIT/GNU’s implementation of scheme. Note from the documentation, that writing begin is often pointless because many special forms already apply it implicitly.

What you need to do, is implement the eval_all() function in scheme_eval_apply.py. Eval_all() takes in two arguments: expressions and env.

You should go through expressions recursively, evaluating each one using scheme_eval(). When you get to the last expression, evaluate it like the others, but also return its value.

For more help

Problem 7: Lambda Procedures

We need to implement the do_lambda_form() function in scheme_forms.py. This function takes in two arguments: expressions and env.

expressions is going to be objects of class Pair representing our formals (just operators for the lambda function) and the second part is the operations.

The variable formals is given to us: formals = expressions.first

What we need to do is take the given information and return a LambdaProcedure object. The LambdaProcedure class is defined in scheme_classes.py. It would be very helpful to review it because you need to initialize and return an object from it.

Hint: LambdaProcedure Class

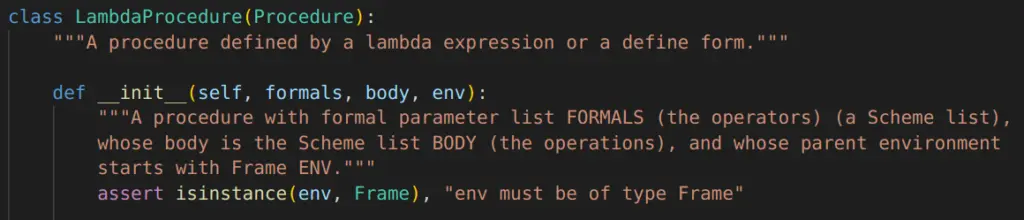
The code you write for this problem should be a single line long

For more help

Problem 8: Making New Frames

In this problem we will be dealing with frames and the creation thereof. When we make a frame, we are initializing an object of class Frame. Each frame has bindings (a dict representing all the variables and values within a frame) and parent (the frame from which the new frame comes from).

In Problem 1 we made the define() method that allowed us to define variables by saving them into the instance variable bindings. ! Remember this !

For Problem 8, we are implementing the class method make_child_frame() which takes in two arguments: formals and vals.

formals is a list of the symbols (the variables to which we are assigning values)

vals is a list of the values we are assigning to the symbols in formals

The CS 111 website gives four steps which are decently clear and pretty much make up the pseudo code for this problem:

For more help

For even more help

And for even more, but less related help

Problem 9: Lambda meets Frame

This is another problem that should not require a lot of code, only two lines to be exact. In scheme_eval_apply.py we have the scheme_apply() function that applies procedures to arguments.

scheme_apply() takes in procedure, args, and env. procedure is going to be an object of class Procedure. It could be a BuiltinProcedure or a LambdaProcedure (MuProcedure or MacroProcedure later too).

args stores the values of the arguments that our procedure is going to be applied to. In the above box it would be the value that replaces the x’s in the LambdaProcedure.

When we make a call to a lambda function, it opens a new frame in which the operators are defined and the operations take place. That means you need to make a new frame whose parent is the current frame. (First Line) Then you need to return an evaluation of all the body of the lambda function (the operations part) using eval_all(). (Second Line)

Unfortunately there is no more help ):

Problem 10: Defining Func’s Shorthandedly

In Problem 10 we are going to edit the do_define_form() function that we wrote a part of in Problem 4. In Problem 4 we made it so that we could assign values to a variable name. Now we want to make it so we can assign functions to a variable name using the following syntax in Scheme:

scm> (define (square x) (* x x))
square
scm> (square 2)
4

do_define_form() takes two arguments: expressions and env. expressions, as normal, is a list of objects from the class Pair. Consider the following example:

You need to dissect expressions to get the function name, the operators, and the operations. Keep in mind we have the variable signature which is equal to the red highlighted portion of expressions above. To define the function we need to take the variable name and assign an object of class LambdaProcedure to it. To create this object we are going to use the function do_lambda_form() from Problem 7.

As a reminder, do_lambda_form() takes in two arguments: expressions and env. It returns an object of class LambdaProcedure. expressions must be a scheme list represented by Pair class objects that hold the operators and the operations. You must create this Pair object in which the first part is the operators and the rest is the operations.

Once you have the LambdaProcedure object, assign it to the variable name in the current frame.

For more help

Problem 11: The ‘Mu’

The first important thing is to understand the difference between lexical and dynamic scoping. Here is the explanation again from the CS 111 website:

First, implement do_mu_form() in scheme_forms.py so that it returns an object of class MuProcedure. This should probably only be one line long. If you need help just look at your code for Problem 7. We are essentially doing the same thing except we are ignoring env because when initializing a MuProcedure we ignore the current frame because of dynamic scoping.

Make sure to look at the __init__() for MuProcedure to see what it intakes as arguments:

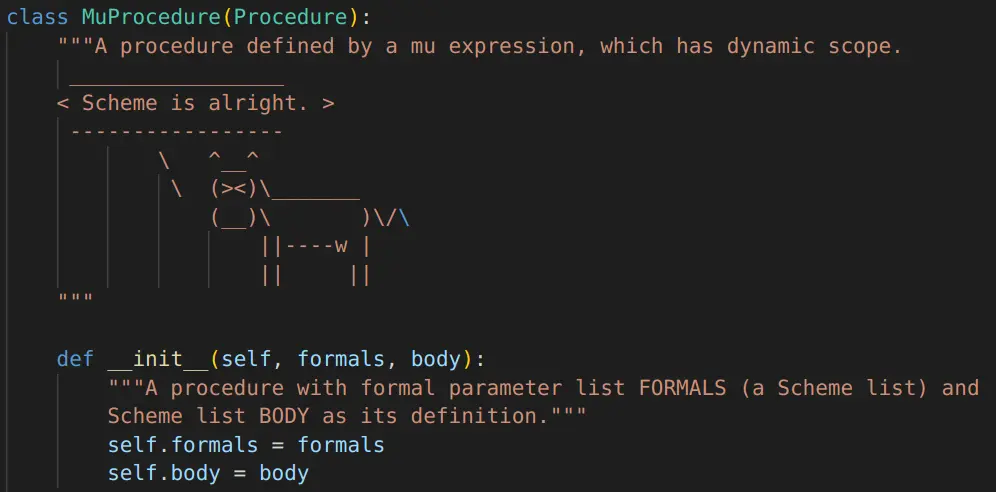
Here are what the arguments to the __init__() would look like if we were initializing a MuProcedure object based off of the given scheme expression:

Second, you need to edit the scheme_apply() function in scheme_eval_apply.py for when the procedure is a MuProcedure. Return the evaluation of the body of the MuProcedure object, but remember you have to do that using the correct frame that results in dynamic scoping. So beforehand make a new frame based off of the current frame. Use this new frame when you evaluate the MuProcedure.

For more help

</end>

Hopefully this was a sufficient help. Please submit any corrections or questions in the comments below. I will try my best to answer and update the article accordingly.

Part 3